Booleaanse algebra. Deel 2. Fundamentele wetten en functies

Vervolg van het verhaal over Booleaanse algebra, conventies, regels, operaties. Overgang naar de basis van contactcircuits.

de eerste artikel George Bull werd beschreven als de maker van de algebra van de logica. Het tweede artikel beschrijft de basisbewerkingen van Booleaanse algebra en methoden voor het vereenvoudigen van Booleaanse uitdrukkingen. Dus, Booleaanse algebra gebruikt verklaringen als argumenten, en niet hun betekenis, maar de waarheid of valsheid van de verklaring.

Het formulier voor het schrijven van uitdrukkingen in Booleaanse algebra.

Als de bewering waar is, wordt deze als volgt geschreven: A = 1, als deze onwaar is, is A = 0 (het is tenslotte niet waar dat aardappel een vrucht is). Voor elke bewering is A waar (A = 1) of onwaar (A = 0). Er kan hier geen midden zijn. We hebben hier al over gesproken.

Als u twee eenvoudige verklaringen verbindt met de unie En, krijgt u een complexe verklaring, die een logisch product wordt genoemd. Laten we twee simpele uitspraken zeggen: "Drie is meer dan twee" zullen we aanwijzen met letter A, "Drie minder dan vijf" - met letter B.

Daarom is de complexe uitspraak "Drie is meer dan twee en minder dan vijf" een logische (in dit geval de hoofdletter En, zegt dat dit een "EN" logische bewerking is, evenals later in de tekst "OF" en "NIET".) en B. Het wordt als volgt aangeduid: A ^ B of A * B.

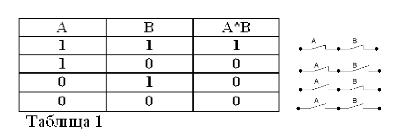
Logische vermenigvuldiging (bewerking "AND").

In elementaire algebra A * A = A2. Maar in Buhl's algebra A * A = A2 = A, A * A = A, omdat het vermenigvuldigingsteken (*) nu betekent ... En ... in de zin van And ... And. Al onze ervaring bevestigt dat A&A hetzelfde is als A. Alleen, men kan het hier niet mee oneens zijn. De waarheid van de verklaring verandert niet als deze meerdere keren door de factor wordt herhaald.

Het product van twee uitspraken wordt dan als waar beschouwd (gelijk aan 1) en alleen als beide factoren waar zijn en onwaar (gelijk aan 0) als ten minste een van de factoren onwaar is. Ben het ermee eens dat deze regels het gezond verstand niet tegenspreken en bovendien volledig voldoen aan de regels van elementaire algebra:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

De eerste gelijkheid luidt als volgt: als zowel A als B waar zijn, is het product A * B waar. In Buhl-algebra vervangt het vermenigvuldigingsteken (*) de unie I.

Logische producten kunnen niet twee, maar een groter aantal verklaringen bevatten - factoren. En in dit geval is het product alleen waar als alle verklaringen-factoren tegelijkertijd waar zijn.

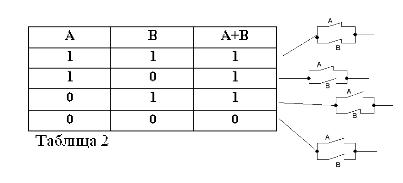
Logische toevoeging (OF-bewerking)

Als twee verklaringen verbonden zijn door een unie OF. die gevormde samengestelde zin een logische som wordt genoemd.

Overweeg een voorbeeld van een logische som. Zeggend A: "Vandaag ga ik naar de bioscoop."

Stelling B: "Vandaag ga ik naar de disco." We voegen beide verklaringen toe en krijgen: "Vandaag ga ik naar de film OF naar een disco."

Deze complexe verklaring wordt als volgt aangegeven: A + B = C of (A V B) = C.

Met C gaven we een complexe verklaring van een logische som aan.

In het onderhavige voorbeeld kan de unie OF niet in exclusieve zin worden gebruikt. Inderdaad, op dezelfde dag kun je naar de bioscoop en naar de disco. En hier is het gezegde:

"De voorzitter van het tuinierspartnerschap zal Petrov of Ivanov zijn", is geen logische som, omdat slechts één persoon de voorzitter zal zijn en de andere een gewone amateur-tuinier.

Het teken V voor de logische som wordt gekozen omdat het de beginletter is van het Latijnse woord "vel", wat "of" betekent, in tegenstelling tot het Latijnse woord "aut>, wat" en "betekent. Nu moet het voor iedereen duidelijk zijn waarom het logische product wordt aangeduid met het teken ^.

In elementaire algebra is er een regel A + A = 2A. Deze regel is waar, ongeacht welk nummer wordt vertegenwoordigd door de letter A. In Booleaanse algebra komt de regel A + A = A overeen. Onze hele levenservaring zegt dat het zeggen van A OF A of beide A gewoon een andere en langere manier is om alleen A te zeggen.

Zoals elke samengestelde bewering, kan de som van de twee beweringen A en B waar of onwaar zijn. De som wordt als waar beschouwd, dat wil zeggen, gelijk aan eenheid, als ten minste een van de voorwaarden waar is:

A + B = 1 als OF A = ​​1 OF B = 1, wat overeenkomt met conventionele rekenkunde:

1+0 = 0+1 = 1.

Als beide samengevatte verklaringen waar zijn, wordt de som ook als waar beschouwd, daarom hebben we in de Booleaanse algebra: (1) + (1) = 1.

De haakjes worden hier geplaatst om het voorwaardelijke, de betekenis van deze toevoeging te benadrukken, en niet het rekenen.

De som van twee verklaringen wordt als onwaar beschouwd en is gelijk aan nul als, maar alleen als beide termen onwaar zijn. Van hier:

0 + 0=0.

Dus de som van de twee uitspraken A + B wordt als waar beschouwd als waar, OF A, OF B, of beide termen samen. Het woord OF wordt dus aangeduid met +.

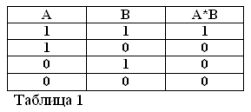
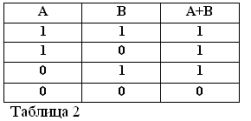
Onthoudend dat beweringen A en B alleen waar of onwaar kunnen zijn en daarom een ​​maat voor waarheid 1 of 0 kunnen hebben, kunnen de resultaten van de beschouwde EN- en OF-bewerkingen worden samengevat in tabellen 1 en 2.

De derde bewerking, die veel wordt gebruikt door Buhl-algebra, is de ontkenningsbewerking - NIET. We herinneren je eraan dat elementaire algebra de bewerkingen TOEVOEGEN, D Aftrekken, Vermenigvuldigen met, Delen door en enkele anderen gebruikt.

Voor elke bewering A is er de ontkenning NIET A, die we zullen aangeven met het symbool / A. Dit mag niet in twijfel worden getrokken.

We geven voorbeelden: "We gaan naar het bos" A, "We gaan niet naar het bos" / A.

Als de bewering A waar is, dat wil zeggen A = 1, dan moet de ontkenning / A onwaar zijn / A = 0. En vice versa, als een bewering onwaar is, dan is de ontkenning waar. Bijvoorbeeld: "Een paard eet geen hooi" / A = 0, "Een paard eet geen hooi" (A = 1). Dit kan worden uitgedrukt in tabel 3.

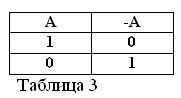
Bepaling van de betekenis van de actie van ontkenning, en aannemend dat van de twee uitspraken A en / A altijd één waar is, volgen twee nieuwe formules van de Booleaanse algebra:

A + (/ A) = 1 en A * (/ A) = 0.

Er zijn ook andere formules die de logische verwerking van instructies vereenvoudigen. Bijvoorbeeld 1 + A = 1, omdat, volgens de definitie van toevoeging, in het geval dat één term gelijk is aan eenheid, de som altijd gelijk is aan eenheid. Het verkregen resultaat hangt niet af van of A = 0 of A = 1.

Elk van de drie logische bewerkingen die we hebben onderzocht (AND, OR, NOT) heeft bepaalde eigenschappen die dicht bij de regels van elementaire algebra liggen. Als ze allemaal zijn geformuleerd, krijgen we 25 regels van Booleaanse algebra. Ze zijn voldoende om bijna elk logisch probleem op te lossen. Zonder deze regels wordt het vrij moeilijk om logische problemen op te lossen vanwege hun schijnbare complexiteit. Proberen om het juiste antwoord te vinden zonder de regels te gebruiken, betekent ze vervangen door vindingrijkheid en algemene redenering. Regels vergemakkelijken dit werk enorm en besparen tijd.

In het kader van het artikel is het onmogelijk om al deze 25 regels in overweging te nemen, maar degenen die dat wensen, kunnen ze altijd in de relevante literatuur vinden.

Zoals reeds vermeld in het eerste artikel in 1938, gebruikt de jonge Amerikaanse wetenschapper Claude Shannon in zijn artikel "Symbolische analyse van relais en schakelkringen" voor het eerst Booleaanse algebra voor problemen met relaistechnologie. Shannons ontdekking was dat hij zich realiseerde dat de methode voor het ontwerpen van relaismachines en elektronische computers eigenlijk een tak van wiskundige logica is.

Het gebeurt vaak. Al vele jaren werkt de wetenschapper aan een probleem dat voor zijn landgenoten volkomen overbodig lijkt - gewoon leuk. Maar tientallen jaren en soms eeuwen verstrijken en een theorie die niemand nodig heeft, verwerft niet alleen het bestaansrecht, maar zonder die verdere vooruitgang wordt ondenkbaar.

Wat hielp Shannon de tweede keer om Booleaanse algebra te 'ontdekken'? De zaak? Niets van dien aard.

De liefde voor relaismachines, gebouwd op conventionele schakelaars en relais, hielp de jonge wetenschapper om een ​​vergeten theorie te verbinden met de taken van automatische telefooncentrales, waaraan hij destijds werkte. Later introduceerde Shannon hetzelfde idee van 'ja of nee' in discrete berichten en legde de basis voor een hele sectie van cybernetica - informatietheorie.

Buhl's algebra was zeer geschikt voor de analyse en synthese van relaisschakelingen. Het was voldoende om te accepteren als een echte uitspraak: "Er is een signaal in het circuit", en als een valse - "Er is geen signaal in het circuit", zoals een nieuwe algebra verscheen - de signaalalgebra, de relaiscircuitalgebra.

De nieuwe algebra is alleen geldig voor het overwegen van relais- en schakelcircuits. Immers, alleen in dergelijke schema's is aan de voorwaarde "er is een signaal" en "geen signaal" voldaan. Wanneer het signaal continu verandert en een willekeurig groot aantal tussenliggende voorwaarden verkrijgt (een dergelijk signaal wordt analoog genoemd), is relay-algebra niet van toepassing. Dit moet altijd worden onthouden. Maar alleen de meeste elektronische computers en cybernetische machines gebruiken het discrete principe van signaalverwerking, dat gebaseerd is op de elementen "ja - nee".

De uitdrukking "Contact gesloten" werd door Shannon geaccepteerd als true (1) en "Contact open" als false (0). De rest van de "algebra", inclusief de operaties EN, OF en NIET en 25 regels, heeft Shannon geleend van Boole.

De relaiscircuitalgebra bleek eenvoudiger te zijn dan de Booleaanse algebra, omdat het alleen elementen van het type "ja - nee" behandelt. Bovendien is de nieuwe algebra visueler.

De elementen in deze algebra zijn de contacten, die we zullen aangeven met de letters A, B, C ... Het contact is gesloten - A, het contact is open - / A (letter met een streepje).

De notatie is, zoals u ziet, volledig overgenomen uit de Booleaanse algebra. Een open contact is een ontkenning van een gesloten contact. Hetzelfde contact kan niet zowel gesloten als open zijn.

Laten we het erover eens zijn dat als in een circuit twee contacten met dezelfde letter worden aangeduid, dit betekent dat ze altijd dezelfde waarden aannemen.

Op elk moment zijn ze beide tegelijkertijd open of beide gesloten. De eenvoudigste manier om u voor te stellen dat ze mechanisch met elkaar verbonden zijn, zodat ze beide tegelijkertijd openen of sluiten.

Als in een bepaalde keten een contact een ontkenning is van een ander contact, dan zijn hun betekenissen altijd tegengesteld. Contacten C en / C kunnen bijvoorbeeld nooit tegelijkertijd open of gelijktijdig gesloten zijn. En in het diagram kunnen ze mechanisch verbonden worden weergegeven: als een van hen opent, sluit de andere.

We beginnen onze kennismaking met relaisalgebra door de eenvoudigste circuits te analyseren die overeenkomen met de EN-, OF- en NIET-bewerkingen.

Het product van twee contacten (bewerking EN) is het circuit dat wordt verkregen als gevolg van hun serieverbinding: het is alleen gesloten (gelijk aan 1) wanneer beide contacten zijn gesloten (gelijk aan 1).

De som van twee contacten (OF-bewerking) is het circuit dat wordt gevormd wanneer ze parallel worden aangesloten: het is gesloten (gelijk aan 1) wanneer ten minste een van de contacten die het circuit vormen gesloten is (gelijk aan 1).

Het tegenovergestelde van dit contact (bewerking NIET) is een contact gelijk aan 0 (open) als dit contact 1 (gesloten) is en vice versa.

Net als in de Booleaanse algebra, als de contacten worden aangeduid met de letters A en B, dan zullen we het product van twee contacten aangeven met A * B, de som met A + B, en het contact tegenover A, met / A. Het bovenstaande wordt uitgelegd in figuren 1, 2 en 3.

Geldigheid van tabellen die overeenkomen met EN-, OF- en NIET-bewerkingen. nu mag niemand twijfelen.

Laten we stilstaan ​​bij twee voorbeelden: 1 * 0 = 0 en 1 + 0 = 1.

In de figuur is te zien dat een permanent gesloten contact in serie verbonden met een permanent open contact gelijk is aan een permanent open contact (1 * 0 = 0). Een permanent gesloten contact parallel verbonden met een permanent open contact is gelijk aan een permanent gesloten contact.

Nadat u vertrouwd bent geraakt met de rekenkunde van contactcircuits, kunt u elk relaiscircuit met een formule beschrijven met behulp van de geaccepteerde conventies. In cybernetica worden dergelijke formules structureel genoemd.

Als de structuurformule van een relaiscircuit 1 is, kan er een signaal doorheen gaan - het circuit is gesloten. En omgekeerd, als de structuurformule van het circuit 0 is, zal het signaal er niet doorheen gaan - het circuit is onderbroken.Conclusie: twee relaiscircuits zijn gelijkwaardig aan elkaar wanneer hun structurele formules gelijk zijn.

In het vervolg van het artikel zullen we voorbeelden van contactcircuits, typische contactcircuits en hun equivalenten beschouwen, evenals diagrammen opstellen volgens structurele formules. We beschouwen ook de belangrijkste logische circuits die de functies van Booleaanse algebra uitvoeren.

Vervolg van het artikel: Booleaanse algebra. Deel 3. Contactschema's

Boris Aladyshkin