Boolen algebra. Osa 2. Peruslait ja toiminnot

Jatko tarinaan Boolen algebrasta, sopimuksista, säännöistä, toiminnoista. Siirtyminen kosketuspiirien perusteisiin.

ensimmäinen artikkeli George Bull kuvattiin logiikan algebran luojaksi. Toisessa artikkelissa kuvataan Boolen algebran perustoiminnot ja menetelmät Boolen lausekkeiden yksinkertaistamiseksi. Joten, Boolen algebra käyttää väitteitä argumentteina eikä niiden merkitystä, vaan lausunnon totuutta tai virheellisyyttä.

Lomake lausekkeiden kirjoittamiseen Boolen algebrassa.

Jos lausunto on totta, niin se kirjoitetaan tällä tavalla: A = 1, jos se on väärä, niin A = 0 (ei ole totta, että peruna on hedelmä). Minkä tahansa lauseen kohdalla A on joko totta (A = 1) tai väärä (A = 0). Täällä ei voi olla keskustaa. Olemme jo puhuneet tästä.

Jos yhdistät kaksi yksinkertaista lauseketta unionin kanssa, saat kompleksisen lausekkeen, jota kutsutaan loogiseksi tuotteeksi. Otetaan kaksi yksinkertaista lausumaa: ”Kolme on enemmän kuin kaksi”, nimitämme kirjaimella A, ”kolme vähemmän kuin viisi” - kirjaimella B.

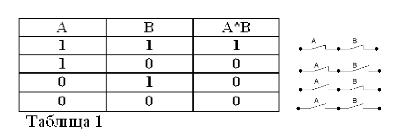
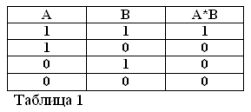
Siksi monimutkainen sanonta "Kolme on enemmän kuin kaksi ja vähemmän kuin viisi" on looginen (tässä tapauksessa iso kirjain I osoittaa, että tämä on "JA" looginen toiminto, samoin kuin myöhemmin tekstissä "TAI" ja "EI"). ja B. Se on merkitty seuraavasti: A ^ B tai A * B.

Looginen kertolasku (operaatio "JA").

Alkuperäisessä algebrassa A * A = A2. Mutta Buhlin algebrassa A * A = A2 = A, A * A = A, koska kertomerkki (*) tarkoittaa nyt ... Ja ... mielessä Ja ... Ja. Kaikki kokemuksemme vahvistavat, että A&A on sama kuin A. yksin. Tähän ei voi olla eri mieltä. Lauseen totuus ei muutu, jos tekijä toistaa sen useita kertoja.

Kahden lauseen tulosta pidetään tosina (yhtä suurena kuin 1), ja vain, jos molemmat tekijät ovat totta, ja vääriksi (yhtä suureiksi kuin 0), jos ainakin yksi tekijöistä on väärä. Hyväksy, että nämä säännöt eivät ole ristiriidassa terveen järjen kanssa, ja lisäksi ne noudattavat täysin ala-algebran sääntöjä:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Ensimmäinen tasa-arvo kuuluu seuraavasti: Jos sekä A että B ovat totta, niin tuote A * B on totta. Buhlin algebralla kertolasku (*) korvaa liiton I.

Loogisissa tuotteissa ei voi olla kahta, vaan enemmän lauseita - tekijöitä. Ja tässä tapauksessa tuote on totta vain, kun samanaikaisesti kaikki väitteet-tekijät ovat totta.

Looginen lisäys (TAI operaatio)

Jos liitto yhdistää kaksi lauseketta TAI. sitä muodostettua yhdistelmälausetta kutsutaan loogiseksi summaksi.

Mieti esimerkki loogisesta summasta. Sanomalla A: "Menen tänään elokuvateatteriin."

Lausunto B: "Menen tänään diskoon." Lisäämme molemmat lausunnot ja saamme: "Tänään menen elokuviin tai diskoon."

Tätä monimutkaista lausumaa merkitään seuraavasti: A + B = C tai (A V B) = C.

C: llä merkitsimme loogisen summan monimutkaista lauseketta.

Tarkasteltavassa esimerkissä liittoa TAI ei voida käyttää yksinoikeudella. Tosiaankin, samana päivänä pääset elokuvateatteriin ja diskoon. Ja tässä on sanonta:

”Puutarhanhoitoyhtiön puheenjohtajana toimii Petrov tai Ivanov”, ei ole looginen summa, koska vain yksi henkilö on puheenjohtaja ja toinen amatööri tavallinen puutarhuri.

Merkki V loogiselle summalle valitaan, koska se on latinalaisen sanan "vel" alkukirjain, joka tarkoittaa "tai", toisin kuin latinalainen sana "aut>", joka tarkoittaa "ja". Nyt kaikille pitäisi olla selvää, miksi looginen tuote on merkitty ^.

Alkuperäisessä algebrassa on sääntö A + A = 2A. Tämä sääntö on totta, riippumatta siitä, mitä numeroa edustaa kirjain A. Boolen algebrassa sääntö A + A = A. Koko elämämme kokemuksemme mukaan sanoa A tai A tai molemmat A on vain toinen ja pidempi tapa sanoa vain A.

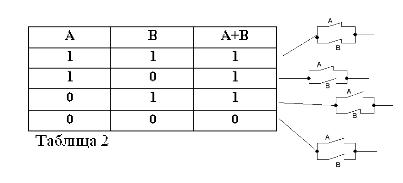
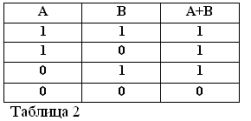
Kuten mikä tahansa yhdistetty lause, kahden lauseen A ja B summa voi olla totta tai vääriä. Summaa pidetään totta, toisin sanoen yhtä suurena, jos ainakin yksi ehdoista on totta:

A + B = 1, jos TAI A = 1 TAI B = 1, mikä on yhdenmukaista tavanomaisen aritmeettisen kanssa:

1+0 = 0+1 = 1.

Jos molemmat summautuneet lausunnot ovat totta, niin summaa pidetään myös totta, joten Boolen algebrassa meillä on: (1) + (1) = 1.

Suluissa on tässä asetettu korostamaan ehdollisuutta, tämän lisäyksen merkitystä eikä aritmeettista.

Kahden lauseen summaa pidetään vääränä ja nollana, jos, mutta vain jos molemmat termit ovat vääriä. Täältä:

0 + 0=0.

Joten kahden lauseen A + B summaa pidetään totta, jos totta, TAI A, TAI B, tai molemmat termit yhdessä. Sanaa OR merkitään siten +.

Kun muistetaan, että lausunnot A ja B voivat olla vain totta tai vääriä ja siten, että niillä voi olla totuuden arvo 1 tai 0, tarkasteltujen JA ja TAI -toimintojen tulokset voidaan tiivistää taulukoihin 1 ja 2.

Kolmas operaatio, jota Buhl algebra käyttää laajasti, on kieltämisoperaatio - EI. Muistutamme, että perusalgebra käyttää toimintoja LISÄ, D Vähennä, Kerro kertoin, Jaa ja, ja jotkut muut.

Jokaisella lauseella A on sen kieltäytyminen EI A, jota merkitsemme symbolilla / A. Tämän ei pitäisi olla epäilystäkään.

Annamme esimerkkejä: “Menemme metsään” A, “Emme mene metsään” / A

Jos lausunto A on totta, ts. A = 1, niin sen kiellon / A on oltava väärä / A = 0. Ja päinvastoin, jos jokin lause on väärä, silloin sen kieltäminen on totta. Esimerkiksi: “Hevonen ei syö heinää” / A = 0, “Hevonen ei syö heinää” (A = 1). Tämä voidaan ilmaista taulukossa 3.

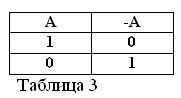
Määrittämällä kieltäytymisen vaikutuksen merkitys ja olettamalla, että kahdesta lauseesta A ja / A on aina yksi totta, seuraavat kaksi Boolen algebran uutta kaavaa:

A + (/ A) = 1 ja A * (/ A) = 0.

On myös muita kaavoja, jotka yksinkertaistavat lauseiden loogista käsittelyä. Esimerkiksi 1 + A = 1, koska lisäyksen määritelmän mukaan siinä tapauksessa, että yksi termi on yhtä suuri, summa on aina yhtä suuri kuin yksikkö. Saatu tulos ei riipu siitä, onko A = 0 vai A = 1.

Jokaisella tutkitulla kolmella loogisella toiminnalla (JA, TAI, EI) on tiettyjä ominaisuuksia, jotka ovat lähellä alkebra-algebran sääntöjä. Jos ne kaikki on muotoiltu, niin saamme 25 Boolen algebran sääntöä. Ne ovat täysin riittäviä ratkaisemaan melkein kaikki loogiset ongelmat. Ilman näitä sääntöjä on melko vaikeaa ratkaista loogisia ongelmia niiden ilmeisen monimutkaisuuden vuoksi. Yritetään löytää oikea vastaus käyttämättä sääntöjä tarkoittaa niiden korvaamista kekseliäisyydellä ja yleisillä perusteluilla. Säännöt helpottavat huomattavasti tätä työtä ja säästävät aikaa.

Artikkelin puitteissa on mahdotonta tarkastella kaikkia näitä 25 sääntöä, mutta haluavat voivat löytää ne aina asiaankuuluvasta kirjallisuudesta.

Kuten jo mainittiin ensimmäisessä artikkelissa vuonna 1938, nuori amerikkalainen tiedemies Claude Shannon kirjoitti artikkelissaan "Releiden ja kytkentäpiirien symbolinen analyysi" ensimmäistä kertaa Boolen algebraa releetekniikan ongelmiin. Shannon löysi, että hän tajusi, että välityslaitteiden ja elektronisten tietokoneiden suunnittelutapa on itse asiassa matemaattisen logiikan haara.

Se tapahtuu usein. Useiden vuosien ajan tiedemies on työskennellyt ongelman parissa, joka vaikuttaa maanmiestensä kannalta täysin tarpeettomalta - vain hauskaa. Mutta vuosikymmeniä ja joskus vuosisatoja kuluu, ja teoria, jota kukaan ei tarvitse, ei vain saa oikeuden olemassaoloon, mutta ilman sitä eteneminen muuttuu mahdottomaksi.

Mikä auttoi Shannonia toisen kerran “löytämään” Boolen algebra? Tapaus? Mitään sellaista.

Perinteisiin kytkimiin ja releisiin rakennettujen välityslaitteiden rakkaus auttoi nuorta tutkijaa yhdistämään unohdetun teorian automaattisten puhelinvaihteiden tehtäviin, joissa hän työskenteli tuolloin. Myöhemmin Shannon esitteli saman idean ”kyllä ​​tai ei” erillisissä viesteissä ja loi perustan koko osaan kybernetiikkaa - informaatioteoriaa.

Buhlin algebra oli erittäin sopiva relepiirien analysointiin ja synteesiin. Se riitti, että se hyväksyttiin oikeana lausumana: ”Piirissä on signaali”, ja vääränä - “Piirissä ei ole signaalia”, koska uusi algebra ilmestyi - signaalialgebra, relepiiri-algebra.

Uusi algebra on voimassa vain rele- ja kytkentäpiirien huomioimiseksi. Loppujen lopuksi vain sellaisissa järjestelmissä ehdot "on signaali" ja "ei signaalia" täyttyvät. Jos signaali muuttuu jatkuvasti, kun saadaan mielivaltaisesti suuri määrä välitilanteita (sellaista signaalia kutsutaan analogiseksi), relealgebra ei ole käytettävissä. Tämä on aina muistettava. Mutta vain suurin osa elektronisista tietokoneista ja kibernetisistä koneista käyttää signaalin käsittelyn diskreettiä periaatetta, joka perustuu elementteihin “kyllä ​​- ei”.

Shannon hyväksyi ilmaisun ”Yhteys suljettu” totta (1) ja ”Yhteys avoin” väärin (0). Loput "algebrasta", mukaan lukien operaatiot JA, TAI ja EI ja 25 sääntöä, Shannon lainasi Boolelta.

Relelähteen algebra osoittautui yksinkertaisemmaksi kuin Boolen algebra, koska se käsittelee vain tyyppejä "kyllä ​​- ei". Lisäksi uusi algebra on visuaalisempi.

Tämän algebran elementit ovat kontakteja, joita merkitsemme kirjaimilla A, B, C ... Yhteys on suljettu - A, kontakti on auki - / A (viiva kirjain).

Merkintä, kuten näette, on kokonaan otettu Boolen algebrasta. Avoin kontakti on suljetun koskettimen kieltäminen. Sama kosketin ei voi olla sekä suljettu että avoin.

Olkaamme yhtä mieltä siitä, että jos missä tahansa piirissä kahta kosketinta merkitään samalla kirjaimella, tämä tarkoittaa, että niillä on aina samat arvot.

Milloin tahansa ne ovat joko molemmat avoinna samanaikaisesti tai molemmat ovat kiinni. Helpoin tapa kuvitella ne mekaanisesti liitettyinä toisiinsa siten, että molemmat avautuvat tai sulkeutuvat samanaikaisesti.

Jos jossain ketjussa kontakti on toisen kosketuksen kieltäminen, silloin niiden merkitykset ovat aina vastakkaiset. Esimerkiksi kontaktit C ja / C eivät koskaan voi olla samanaikaisesti avoinna tai suljettu samanaikaisesti. Ja kaaviossa ne voidaan esittää mekaanisesti kytkettynä: jos yksi niistä avautuu, toinen sulkeutuu.

Aloitamme tutustumisen relealgebraan analysoimalla yksinkertaisimpia piirejä, jotka vastaavat AND-, OR- ja NOT-toimintoja.

Kahden koskettimen (toiminta JA) tulos on piiri, joka saadaan niiden sarjayhteyden tuloksena: se on suljettu (yhtä suuri kuin 1) vain, kun molemmat koskettimet ovat kiinni (yhtä kuin 1).

Kahden koskettimen (TAI toiminta) summa on piiri, joka muodostuu, kun ne on kytketty rinnakkain: se on suljettu (yhtä suuri kuin 1), kun ainakin yksi piirin muodostavista koskettimista on suljettu (yhtä suuri kuin 1).

Tämän koskettimen vastakohta (toiminta EI) on kosketin, joka on yhtä suuri kuin 0 (avoin), jos tämä kosketin on 1 (suljettu), ja päinvastoin.

Kuten Boolen algebrassa, jos koskettimet on merkitty kirjaimilla A ja B, niin merkitsemme kahden kontaktin tulosta A * B: llä, summan A + B: llä ja A: ta vastakkaisella koskettimella / A: lla. Edellä selitetään kuvioissa 1, 2 ja 3.

AND-, OR- ja NOT-operaatioita vastaavien taulukoiden voimassaolo. nyt kukaan ei saa olla epävarma.

Pitäkäämme kiinni kahdesta esimerkistä: 1 * 0 = 0 ja 1 + 0 = 1.

Kuviosta voidaan nähdä, että pysyvästi suljettu kosketin, joka on kytketty sarjaan jatkuvasti avoimen koskettimen kanssa, vastaa pysyvästi avointa kosketinta (1 * 0 = 0) Pysyvästi suljettu kosketin, joka on kytketty jatkuvasti avoimen koskettimen kanssa, vastaa pysyvästi suljettua kosketinta.

Tuttuaan kosketuspiirien aritmeettisen osaamisen, voit kuvailla mitä tahansa relepiiriä kaavalla käyttämällä hyväksyttyjä käytäntöjä. Kybernetiikassa sellaisia ​​kaavoja kutsutaan rakenteellisiksi.

Jos minkä tahansa relepiirin rakennekaava on 1, signaali voi kulkea sen läpi - piiri on suljettu. Ja päinvastoin, jos piirin rakennekaava on 0, signaali ei kulje sen läpi - piiri on rikki.Johtopäätös: kaksi relepiiriä ovat ekvivalentteja toisiinsa, kun niiden rakennekaavat ovat samat.

Artikkelin jatkossa tarkastelemme esimerkkejä kosketuspiireistä, tyypillisistä kosketuspiireistä ja niiden vastaavista, sekä laatimme kaavioita rakennekaavojen mukaisesti. Tarkastelemme myös päälogiikkapiirejä, jotka suorittavat Boolen algebran toimintoja.

Artikkelin jatko: Boolen algebra. Osa 3. Yhteysjärjestelmät

Boris Aladyshkin