Álgebra booleana. Parte 2. Leyes y funciones básicas.

Continuación de la historia sobre álgebra booleana, convenciones, reglas, operaciones. Transición a lo básico de los circuitos de contacto.

En primer articulo George Bull fue descrito como el creador del álgebra de la lógica. El segundo artículo describirá las operaciones básicas del álgebra booleana y los métodos para simplificar las expresiones booleanas. Entonces, el álgebra booleana usa declaraciones como argumentos, y no su significado, sino la verdad o falsedad de la declaración.

La forma de escribir expresiones en álgebra booleana.

Si la afirmación es verdadera, entonces se escribe así: A = 1, si es falsa, entonces A = 0 (después de todo, no es cierto que la papa sea una fruta). Para cualquier enunciado, A es verdadero (A = 1) o falso (A = 0). No puede haber un medio aquí. Ya hemos hablado de esto.

Si conecta dos declaraciones simples con la unión Y, obtiene una declaración compleja, que se llama un producto lógico. Tomemos dos dichos simples: "Tres es más que dos" designaremos con la letra A, "Tres menos que cinco" - con la letra B.

Por lo tanto, la afirmación compleja "Tres es más de dos y menos de cinco" es lógica (en este caso, la letra mayúscula Y, dice que esta es una operación lógica "Y", así como más adelante en el texto "O" y "NO"). y B. Se designa de la siguiente manera: A ^ B o A * B.

Multiplicación lógica (operación "Y").

En álgebra elemental A * A = A2. Pero en el álgebra de Buhl A * A = A2 = A, A * A = A, ya que el signo de multiplicación (*) ahora significa ... Y ... en el sentido de Y ... Y. Toda nuestra experiencia confirma que A&A es lo mismo que A. solo. Uno no puede estar en desacuerdo con esto. La verdad de la declaración no cambia si el factor la repite varias veces.

El producto de dos afirmaciones se considera verdadero (igual a 1), entonces, y solo si ambos factores son verdaderos, y falso (igual a 0) si al menos uno de los factores es falso. Acuerde que estas reglas no contradicen el sentido común y, además, cumplen totalmente con las reglas del álgebra elemental:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

La primera igualdad dice lo siguiente: si A y B son verdaderas, entonces el producto A * B es verdadero. En álgebra de Buhl, el signo de multiplicación (*) reemplaza la unión I.

Los productos lógicos pueden incluir no dos, sino un mayor número de declaraciones: factores. Y en este caso, el producto es verdadero solo cuando al mismo tiempo todos los factores de afirmación son verdaderos.

Adición lógica (operación OR)

Si dos declaraciones están conectadas por una unión O. esa oración compuesta formada se llama suma lógica.

Considere un ejemplo de una suma lógica. Decir A: "Hoy iré al cine".

Declaración B: "Hoy iré a la discoteca". Agregamos ambas declaraciones y obtenemos: "Hoy iré al cine O a una discoteca".

Esta declaración compleja se denota de la siguiente manera: A + B = C o (A V B) = C.

Por C denotamos una declaración compleja de una suma lógica.

En el ejemplo bajo consideración, la unión O no se puede usar en un sentido exclusivo. De hecho, el mismo día puedes ir al cine y a la discoteca. Y aquí está el dicho:

"El presidente de la asociación de jardinería será Petrov o Ivanov", no es una suma lógica, porque solo una persona será el presidente y la otra será un jardinero aficionado.

El signo V para la suma lógica se elige porque es la letra inicial de la palabra latina "vel", que significa "o", en contraste con la palabra latina "aut>, que significa" y ". Ahora debería quedar claro para todos por qué el producto lógico está indicado por el signo ^.

En álgebra elemental hay una regla A + A = 2A. Esta regla es verdadera, no importa qué número esté representado por la letra A. En álgebra booleana, la regla A + A = A corresponde a ella. Toda nuestra experiencia de vida dice que decir A OR A o ambos A es solo otra forma más larga de decir solo A.

Al igual que cualquier declaración compuesta, la suma de las dos declaraciones A y B puede ser verdadera o falsa. La suma se considera verdadera, es decir, igual a la unidad, si al menos uno de los términos es verdadero:

A + B = 1 si OR A = 1 OR B = 1, que es consistente con la aritmética convencional:

1+0 = 0+1 = 1.

Si ambas declaraciones sumadas son verdaderas, entonces la suma también se considera verdadera, por lo tanto, en el álgebra booleana tenemos: (1) + (1) = 1.

Los corchetes se establecen aquí para enfatizar el condicional, el significado de esta adición y no la aritmética.

La suma de dos declaraciones se considera falsa e igual a cero si, pero solo si ambos términos son falsos. Desde aquí:

0 + 0=0.

Entonces, la suma de las dos declaraciones A + B se considera verdadera si es verdadera, OR A, OR B, OR ambos términos juntos. Por lo tanto, la palabra OR se denota por +.

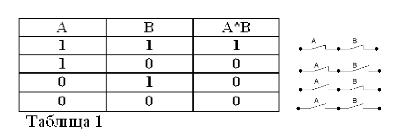
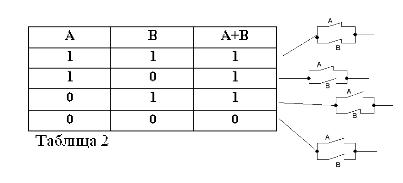
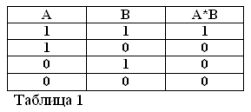
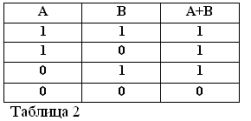
Recordando que las declaraciones A y B solo pueden ser verdaderas o falsas y, por lo tanto, tener una medida de verdad 1 o 0, los resultados de las operaciones AND y OR consideradas se pueden resumir en las tablas 1 y 2.

La tercera operación, ampliamente utilizada por el álgebra de Buhl, es la operación de negación, NO. Le recordamos que el álgebra elemental usa las operaciones AGREGAR, D Restar, Multiplicar por, Dividir por y algunas otras.

Para cada enunciado A, existe su negación NO A, que denotaremos con el símbolo / A. Esto no debería estar en duda.

Damos ejemplos: "Iremos al bosque" A, "No iremos al bosque" / A.

Si la afirmación A es verdadera, es decir, A = 1, entonces su negación / A debe ser falsa / A = 0. Y viceversa, si alguna afirmación es falsa, entonces su negación es verdadera. Por ejemplo: “Un caballo no come heno” / A = 0, “Un caballo no come heno” (A = 1). Esto se puede expresar en la tabla 3.

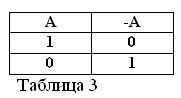
Al determinar el significado de la acción de negación, y asumiendo que el de las dos declaraciones A y / A es siempre una verdadera, siguen dos nuevas fórmulas de álgebra booleana:

A + (/ A) = 1 y A * (/ A) = 0.

También hay otras fórmulas que simplifican el procesamiento lógico de las declaraciones. Por ejemplo, 1 + A = 1, ya que, según la definición de suma, en el caso de que un término sea igual a la unidad, la suma siempre es igual a la unidad. El resultado obtenido no depende de si A = 0 o A = 1.

Cada una de las tres operaciones lógicas que examinamos (AND, OR, NOT) tiene ciertas propiedades que están cerca de las reglas del álgebra elemental. Si todos están formulados, obtenemos 25 reglas de álgebra booleana. Son suficientes para resolver casi cualquier problema lógico. Sin estas reglas, se vuelve bastante difícil resolver problemas lógicos debido a su aparente complejidad. Intentar encontrar la respuesta correcta sin usar las reglas significa reemplazarlas con ingenio y razonamiento general. Las reglas facilitan enormemente este trabajo y ahorran tiempo.

En el marco del artículo, es imposible considerar todas estas 25 reglas, pero aquellos que lo deseen siempre pueden encontrarlas en la literatura relevante.

Como ya se mencionó en el primer artículo en 1938, el joven científico estadounidense Claude Shannon en su artículo "Análisis simbólico de relés y circuitos de conmutación" por primera vez utiliza álgebra booleana para problemas de tecnología de relés. El descubrimiento de Shannon fue que se dio cuenta de que el método de diseñar máquinas de retransmisión y computadoras electrónicas es en realidad una rama de la lógica matemática.

A menudo sucede Durante muchos años, el científico ha estado trabajando en un problema que parece completamente innecesario para sus compatriotas, simplemente divertido. Pero pasan décadas y, a veces, siglos, y una teoría que nadie necesita no solo adquiere el derecho a existir, sino que sin ella, el progreso se vuelve impensable.

¿Qué ayudó a Shannon por segunda vez a "descubrir" el álgebra booleana? Caso? Nada de eso.

El amor por las máquinas de retransmisión, basadas en interruptores y relés convencionales, ayudó al joven científico a conectar una teoría olvidada con las tareas de las centrales telefónicas automáticas, en las que trabajó en ese momento. Más tarde, Shannon introdujo la misma idea de "sí o no" en mensajes discretos y sentó las bases para toda una sección de cibernética: teoría de la información.

El álgebra de Buhl fue muy adecuado para el análisis y síntesis de circuitos de relé. Fue suficiente para aceptar como una declaración verdadera: "Hay una señal en el circuito", y como una falsa: "No hay señal en el circuito", como apareció un nuevo álgebra: la señal de álgebra, el álgebra del circuito de relé.

El nuevo álgebra es válido solo para la consideración de relés y circuitos de conmutación. Después de todo, solo en tales esquemas se cumple la condición "hay señal" y "sin señal". Cuando la señal cambia continuamente, adquiriendo un número arbitrariamente grande de condiciones intermedias (tal señal se llama analógica), el álgebra de relevo no es aplicable. Esto siempre debe ser recordado. Pero solo la mayoría de las computadoras electrónicas y las máquinas cibernéticas utilizan el principio discreto del procesamiento de señales, que se basa en los elementos "sí - no".

Shannon aceptó la expresión "Contacto cerrado" como verdadero (1) y "Contacto abierto" como falso (0). El resto del "álgebra", incluidas las operaciones AND, OR y NOT y 25 reglas, Shannon tomó prestado de Boole.

El álgebra del circuito de relé resultó ser más simple que el álgebra booleana, ya que solo trata con elementos del tipo "sí - no". Además, el nuevo álgebra es más visual.

Los elementos en este álgebra son los contactos, que denotaremos con las letras A, B, C ... El contacto está cerrado - A, el contacto está abierto - / A (letra con un guión).

La notación, como puede ver, está completamente tomada del álgebra booleana. Un contacto abierto es una negación de un contacto cerrado. El mismo contacto no puede ser cerrado y abierto.

Acordemos que si en cualquier circuito dos contactos se denotan con la misma letra, esto significa que siempre toman los mismos valores.

En cualquier momento, ambos están abiertos al mismo tiempo o ambos están cerrados. La forma más fácil de imaginarlos conectados mecánicamente para que ambos se abran o cierren simultáneamente.

Si en alguna cadena un contacto es una negación de otro contacto, entonces sus significados son siempre opuestos. Por ejemplo, los contactos C y / C nunca pueden abrirse o cerrarse simultáneamente. Y en el diagrama pueden representarse conectados mecánicamente: si uno de ellos se abre, el otro se cierra.

Comenzamos a conocer el álgebra de relevos analizando los circuitos más simples correspondientes a las operaciones AND, OR y NOT.

El producto de dos contactos (operación Y) es el circuito obtenido como resultado de su conexión en serie: está cerrado (igual a 1) solo cuando ambos contactos están cerrados (igual a 1).

La suma de dos contactos (operación OR) será el circuito formado cuando estén conectados en paralelo: está cerrado (igual a 1) cuando al menos uno de los contactos que forman el circuito está cerrado (igual a 1).

Lo contrario de este contacto (operación NO) es un contacto igual a 0 (abierto) si este contacto es 1 (cerrado), y viceversa.

Como en el álgebra booleana, si los contactos se denotan con las letras A y B, entonces denotaremos el producto de dos contactos por A * B, la suma por A + B y el contacto opuesto a A, por / A. Lo anterior se explica en las Figuras 1, 2 y 3.

Validez de las tablas correspondientes a las operaciones AND, OR y NOT. ahora nadie debería tener dudas.

Detengámonos en dos ejemplos: 1 * 0 = 0 y 1 + 0 = 1.

Se puede ver en la figura que un contacto permanentemente cerrado conectado en serie con un contacto permanentemente abierto es equivalente a un contacto permanentemente abierto (1 * 0 = 0) Un contacto permanentemente cerrado conectado en paralelo con un contacto permanentemente abierto es equivalente a un contacto permanentemente cerrado.

Habiéndose familiarizado con la aritmética de los circuitos de contacto, puede describir cualquier circuito de relé con una fórmula utilizando las convenciones aceptadas. En cibernética, tales fórmulas se llaman estructurales.

Si la fórmula estructural de cualquier circuito de relé es 1, entonces una señal puede pasar a través de él: el circuito está cerrado. Y viceversa, si la fórmula estructural del circuito es 0, la señal no pasará a través de él, el circuito está roto.Conclusión: dos circuitos de relé son equivalentes entre sí cuando sus fórmulas estructurales son iguales.

En la continuación del artículo, consideraremos ejemplos de circuitos de contacto, circuitos de contacto típicos y sus equivalentes, así como también dibujaremos diagramas de acuerdo con fórmulas estructurales. También consideramos los principales circuitos lógicos que realizan las funciones de álgebra booleana.

Continuación del artículo: Álgebra booleana. Parte 3. Esquemas de contacto

Boris Aladyshkin