Boolean algebra. Part 2. Basic laws and functions

Continuation of the story about Boolean algebra, conventions, rules, operations. Transition to the basics of contact circuits.

IN first article George Bull was described as the creator of the algebra of logic. The second article will describe the basic operations of Boolean algebra, and methods for simplifying Boolean expressions. So, Boolean algebra uses statements as arguments, and not their meaning, but the truth or falsity of the statement.

The form for writing expressions in Boolean algebra.

If the statement is true, then it is written like this: A = 1, if it is false, then A = 0 (after all, it is not true that potato is a fruit). For any statement, A is either true (A = 1) or false (A = 0). There can be no middle here. We have already talked about this.

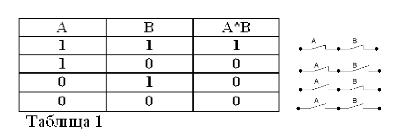
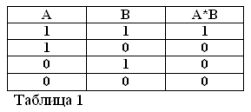
If you connect two simple statements with the union And, you get a complex statement, which is called a logical product. Let's take two simple sayings: “Three is more than two” we will designate by letter A, “Three less than five” - by letter B.

Hence the complex saying “Three is more than two And less than five” is a logical one (in this case, the capital letter I indicates that this is an “AND” logical operation, as well as later in the text “OR” and “NOT.”) and B. It is designated as follows: A ^ B or A * B.

Logical multiplication (operation "AND").

In elementary algebra A * A = A2. But in Buhl’s algebra A * A = A2 = A, A * A = A, since the multiplication sign (*) now means ... And ... in the sense of And ... And. All our experience confirms that A&A is the same as A. alone. One cannot disagree with this. The truth of the statement does not change if it is repeated by the factor several times.

The product of two statements is considered true (equal to 1), then, and only if both factors are true, and false (equal to 0) if at least one of the factors is false. Agree that these rules do not contradict common sense, and, in addition, they fully comply with the rules of elementary algebra:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

The first equality reads as follows: if both A and B are true, then the product A * B is true. In Buhl algebra, the multiplication sign (*) replaces the union I.

Logical products may include not two, but a greater number of statements - factors. And in this case, the product is true only when at the same time all statements-factors are true.

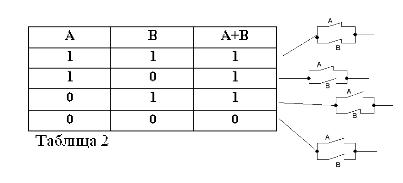
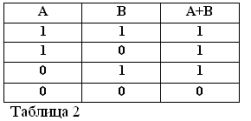
Logical addition (OR operation)

If two statements are connected by a union OR. that formed compound sentence is called a logical sum.

Consider an example of a logical sum. Saying A: "Today I will go to the cinema."

Statement B: “Today I will go to the disco.” We add both statements and get: "Today I will go to the movies OR to a disco."

This complex statement is denoted as follows: A + B = C or (A V B) = C.

By C we denoted a complex statement of a logical sum.

In the example under consideration, the union OR cannot be used in an exclusive sense. Indeed, on the same day you can get to the cinema and to the disco. And here is the saying:

“The chairman of the gardening partnership will be Petrov or Ivanov” —not a logical sum, because only one person will be the chairman, and the other will be an amateur ordinary gardener.

The sign V for the logical sum is chosen because it is the initial letter of the Latin word "vel", meaning "or", in contrast to the Latin word "aut>, which means" and ". Now it should be clear to everyone why the logical product is indicated by the sign ^.

In elementary algebra there is a rule A + A = 2A. This rule is true, no matter what number is represented by the letter A. In Boolean algebra, the rule A + A = A corresponds to it. Our whole life experience says that to say A OR A or both A is just another and longer way to say just A.

Like any compound statement, the sum of the two statements A and B can be true or false. The sum is considered true, that is, equal to unity, if at least one of the terms is true:

A + B = 1 if OR A = 1 OR B = 1, which is consistent with conventional arithmetic:

1+0 = 0+1 = 1.

If both summed statements are true, then the sum is also considered true, therefore, in the Boolean algebra we have: (1) + (1) = 1.

The brackets are set here in order to emphasize the conditional, the meaning of this addition, and not arithmetic.

The sum of two statements is considered false and equal to zero if, but only if both terms are false. From here:

0 + 0=0.

So, the sum of the two statements A + B is considered true if true, OR A, OR B, OR both terms together. Thus, the word OR is denoted by +.

Remembering that statements A and B can only be true or false and, therefore, have a measure of truth 1 or 0, the results of the considered AND and OR operations can be summarized in tables 1 and 2.

The third operation, widely used by Buhl algebra, is the negation operation - NOT. We remind you that elementary algebra uses the operations ADD, D Subtract, Multiply by, Divide by, and some others.

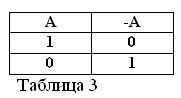
For each statement A, there is its negation NOT A, which we will denote by the symbol / A. This should not be in doubt.

We give examples: “We will go to the forest” A, “We will not go to the forest” / A.

If the statement A is true, that is, A = 1, then its negation / A must be false / A = 0. And vice versa, if any statement is false, then its negation is true. For example: “A horse does not eat hay” / A = 0, “A horse does not eat hay” (A = 1). This can be expressed in table 3.

Determining the meaning of the action of negation, and assuming that of the two statements A and / A is always one true, two new formulas of the Boolean algebra follow:

A + (/ A) = 1 and A * (/ A) = 0.

There are also other formulas that simplify the logical processing of statements. For example, 1 + A = 1, since, according to the definition of addition, in the case when one term is equal to unity, the sum is always equal to unity. The result obtained does not depend on whether A = 0 or A = 1.

Each of the three logical operations we examined (AND, OR, NOT) has certain properties that are close to the rules of elementary algebra. If all of them are formulated, then we get 25 rules of Boolean algebra. They are quite enough to solve almost any logical problem. Without these rules, it becomes quite difficult to solve logical problems because of their apparent complexity. Trying to find the correct answer without using the rules means replacing them with ingenuity and general reasoning. Rules greatly facilitate this work and save time.

Within the framework of the article, it is impossible to consider all these 25 rules, but those who wish can always find them in the relevant literature.

As already mentioned in the first article in 1938, the young American scientist Claude Shannon in his article “Symbolic Analysis of Relay and Switching Circuits” for the first time uses Boolean algebra for problems of relay technology. Shannon's discovery was that he realized that the method of designing relay machines and electronic computers is actually a branch of mathematical logic.

It happens often. For many years, the scientist has been working on a problem that seems completely unnecessary to his compatriots - just fun. But decades and sometimes centuries pass, and a theory that no one needs does not only acquire the right to exist, but without it further progress becomes unthinkable.

What helped Shannon second time “discover” Boolean algebra? Happening? Nothing like this.

The love of relay machines, built on conventional switches and relays, helped the young scientist to connect a forgotten theory with the tasks of automatic telephone exchanges, on which he worked at that time. Subsequently, Shannon introduced the same idea of ​​“yes or no” into discrete messages and laid the foundation for a whole section of cybernetics — information theory.

Buhl's algebra was very suitable for the analysis and synthesis of relay circuits. It was enough to accept as a true statement: “There is a signal in the circuit”, and as a false one - “There is no signal in the circuit”, as a new algebra appeared - the signal algebra, the relay circuit algebra.

The new algebra is valid only for the consideration of relay and switching circuits. After all, only in such schemes is the condition “there is a signal” and “no signal” satisfied. Where the signal changes continuously, acquiring an arbitrarily large number of intermediate conditions (such a signal is called analog), relay algebra is not applicable. This must always be remembered. But just the majority of electronic computers and cybernetic machines use the discrete principle of signal processing, which is based on the elements “yes - no”.

The expression “Contact closed” was accepted by Shannon as true (1), and “Contact open” as false (0). The rest of the "algebra", including the operations AND, OR and NOT and 25 rules, Shannon borrowed from Boole.

The relay circuit algebra turned out to be simpler than the Boolean algebra, since it deals only with elements of the "yes - no" type. In addition, the new algebra is more visual.

The elements in this algebra are the contacts, which we will denote by the letters A, B, C ... The contact is closed - A, the contact is open - / A (letter with a dash).

The notation, as you see, is completely taken from Boolean algebra. An open contact is a negation of a closed contact. The same contact cannot be both closed and open.

Let us agree that if in any circuit two contacts are denoted by the same letter, this means that they always take the same values.

At any given moment, they are either both open at the same time, or both are closed. The easiest way to imagine them mechanically connected together so that both of them simultaneously open or close.

If in some chain a contact is a negation of another contact, then their meanings are always opposite. For example, contacts C and / C can never be simultaneously open or simultaneously closed. And in the diagram they can be represented mechanically connected: if one of them opens, then the other closes.

We begin our acquaintance with relay algebra by analyzing the simplest circuits corresponding to the AND, OR, and NOT operations.

The product of two contacts (operation AND) is the circuit obtained as a result of their series connection: it is closed (equal to 1) only when both contacts are closed (equal to 1).

The sum of two contacts (OR operation) will be the circuit formed when they are connected in parallel: it is closed (equal to 1) when at least one of the contacts forming the circuit is closed (equal to 1).

The opposite of this contact (operation NOT) is a contact equal to 0 (open) if this contact is 1 (closed), and vice versa.

As in the Boolean algebra, if the contacts are denoted by the letters A and B, then we will denote the product of two contacts by A * B, the sum by A + B, and the contact opposite A, by / A. The above is explained in Figures 1, 2, and 3.

Validity of tables corresponding to AND, OR, and NOT operations. now no one should be in doubt.

Let us dwell on two examples: 1 * 0 = 0 and 1 + 0 = 1.

It can be seen from the figure that a permanently closed contact connected in series with a permanently open contact is equivalent to a permanently open contact (1 * 0 = 0) A permanently closed contact connected in parallel with a constantly open contact is equivalent to a permanently closed contact.

Having become acquainted with the arithmetic of contact circuits, you can describe any relay circuit with a formula using the accepted conventions. In cybernetics, such formulas are called structural.

If the structural formula of any relay circuit is 1, then a signal can pass through it - the circuit is closed. Conversely, if the structural formula of the circuit is 0, the signal will not pass through it - the circuit is broken.Conclusion: two relay circuits are equivalent to each other when their structural formulas are equal.

In the continuation of the article, we will consider examples of contact circuits, typical contact circuits and their equivalents, as well as drawing up diagrams according to structural formulas. We also consider the main logic circuits that perform the functions of Boolean algebra.

Continuation of the article: Boolean algebra. Part 3. Contact schemes

Boris Aladyshkin