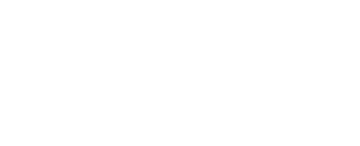Boolesche Algebra. Teil 2. Grundgesetze und Funktionen

Fortsetzung der Geschichte über Boolesche Algebra, Konventionen, Regeln, Operationen. Übergang zu den Grundlagen der Kontaktschaltungen.

In erster Artikel George Bull wurde als Schöpfer der Algebra der Logik beschrieben. Der zweite Artikel beschreibt die grundlegenden Operationen der Booleschen Algebra und Methoden zur Vereinfachung der Booleschen Ausdrücke. Die boolesche Algebra verwendet also Aussagen als Argumente und nicht deren Bedeutung, sondern die Wahrheit oder Falschheit der Aussage.

Das Formular zum Schreiben von Ausdrücken in der Booleschen Algebra.

Wenn die Aussage wahr ist, dann lautet sie wie folgt: A = 1, wenn sie falsch ist, dann ist A = 0 (es ist nicht wahr, dass Kartoffel eine Frucht ist). Für jede Aussage ist A entweder wahr (A = 1) oder falsch (A = 0). Hier kann es keine Mitte geben. Wir haben bereits darüber gesprochen.

Wenn Sie zwei einfache Anweisungen mit der Vereinigung And verbinden, erhalten Sie eine komplexe Anweisung, die als logisches Produkt bezeichnet wird. Nehmen wir zwei einfache Sprüche: "Drei ist mehr als zwei" werden wir mit Buchstabe A bezeichnen, "Drei weniger als fünf" - mit Buchstabe B.

Daher ist die komplexe Aussage „Drei ist mehr als zwei und weniger als fünf“ eine logische Eins (in diesem Fall sagt der Großbuchstabe Und, dass dies eine logische „UND“ -Operation ist, sowie später im Text „ODER“ und „NICHT“). und B. Es wird wie folgt bezeichnet: A ^ B oder A * B.

Logische Multiplikation (Operation "UND").

In der Elementaralgebra ist A * A = A2. Aber in Buhls Algebra ist A * A = A2 = A, A * A = A, da das Multiplikationszeichen (*) jetzt bedeutet ... und ... im Sinne von Und ... Und. Alle unsere Erfahrungen bestätigen, dass A & A dasselbe ist wie A. allein. Dem kann man nicht widersprechen. Die Wahrheit der Aussage ändert sich nicht, wenn sie durch den Faktor mehrmals wiederholt wird.

Das Produkt zweier Aussagen wird dann als wahr (gleich 1) und nur dann betrachtet, wenn beide Faktoren wahr sind, und falsch (gleich 0), wenn mindestens einer der Faktoren falsch ist. Stimmen Sie zu, dass diese Regeln nicht dem gesunden Menschenverstand widersprechen und darüber hinaus den Regeln der Elementaralgebra vollständig entsprechen:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Die erste Gleichheit lautet wie folgt: Wenn sowohl A als auch B wahr sind, ist das Produkt A * B wahr. In der Buhl-Algebra ersetzt das Multiplikationszeichen (*) die Vereinigung I.

Logische Produkte können nicht zwei, sondern eine größere Anzahl von Aussagen enthalten - Faktoren. Und in diesem Fall ist das Produkt nur dann wahr, wenn alle Aussagenfaktoren gleichzeitig wahr sind.

Logische Addition (ODER-Verknüpfung)

Wenn zwei Anweisungen durch eine Vereinigung ODER verbunden sind. Dieser gebildete zusammengesetzte Satz wird als logische Summe bezeichnet.

Betrachten Sie ein Beispiel für eine logische Summe. A sagen: "Heute gehe ich ins Kino."

Aussage B: "Heute gehe ich in die Disco." Wir fügen beide Aussagen hinzu und erhalten: "Heute gehe ich ins Kino ODER in eine Disco."

Diese komplexe Aussage wird wie folgt bezeichnet: A + B = C oder (A V B) = C.

Mit C haben wir eine komplexe Aussage einer logischen Summe bezeichnet.

In dem betrachteten Beispiel kann das Vereinigungs-ODER nicht in einem ausschließlichen Sinne verwendet werden. In der Tat können Sie am selben Tag ins Kino und in die Disco gehen. Und hier ist das Sprichwort:

„Der Vorsitzende der Gartenpartnerschaft wird Petrow oder Iwanow sein“ - keine logische Summe, da nur eine Person der Vorsitzende und die andere ein gewöhnlicher Amateurgärtner sein wird.

Das Vorzeichen V für die logische Summe wird gewählt, weil es der Anfangsbuchstabe des lateinischen Wortes "vel" ist, was "oder" bedeutet, im Gegensatz zum lateinischen Wort "aut>", was "und" bedeutet. Jetzt sollte allen klar sein, warum das logische Produkt durch das Zeichen ^ gekennzeichnet ist.

In der Elementaralgebra gibt es eine Regel A + A = 2A. Diese Regel ist wahr, egal welche Zahl durch den Buchstaben A dargestellt wird. In der Booleschen Algebra entspricht die Regel A + A = A dieser. Unsere gesamte Lebenserfahrung besagt, dass A oder A oder beides A nur eine andere und längere Art ist, nur A zu sagen.

Wie bei jeder zusammengesetzten Aussage kann die Summe der beiden Aussagen A und B wahr oder falsch sein. Die Summe wird als wahr angesehen, dh gleich Eins, wenn mindestens einer der Begriffe wahr ist:

A + B = 1, wenn OR A = 1 ODER B = 1, was mit der herkömmlichen Arithmetik übereinstimmt:

1+0 = 0+1 = 1.

Wenn beide summierten Aussagen wahr sind, wird die Summe auch als wahr angesehen, daher haben wir in der Booleschen Algebra: (1) + (1) = 1.

Die Klammern werden hier gesetzt, um die Bedingung, die Bedeutung dieser Addition und nicht die Arithmetik hervorzuheben.

Die Summe zweier Aussagen wird nur dann als falsch und gleich Null betrachtet, wenn beide Begriffe falsch sind. Von hier aus:

0 + 0=0.

Die Summe der beiden Aussagen A + B wird also als wahr angesehen, wenn wahr, ODER A, ODER B ODER beide Begriffe zusammen. Somit wird das Wort OR mit + bezeichnet.

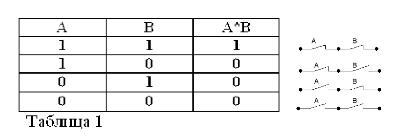
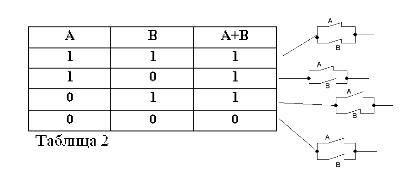
Wenn man bedenkt, dass die Aussagen A und B nur wahr oder falsch sein können und daher ein Maß für die Wahrheit 1 oder 0 haben, können die Ergebnisse der betrachteten UND- und ODER-Operationen in den Tabellen 1 und 2 zusammengefasst werden.

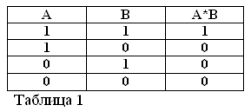
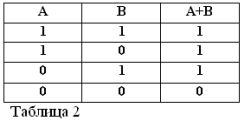
Die dritte Operation, die in der Buhl-Algebra weit verbreitet ist, ist die Negationsoperation - NICHT. Wir erinnern Sie daran, dass die Elementaralgebra die Operationen ADD, D Subtrahieren, Multiplizieren mit, Teilen durch und einige andere verwendet.

Für jede Aussage A gibt es ihre Negation NICHT A, die wir mit dem Symbol / A bezeichnen werden. Dies sollte kein Zweifel sein.

Wir geben Beispiele: „Wir werden in den Wald gehen“ A, „Wir werden nicht in den Wald gehen“ / A.

Wenn die Aussage A wahr ist, dh A = 1, dann muss ihre Negation / A falsch sein / A = 0. Und umgekehrt, wenn eine Aussage falsch ist, dann ist ihre Negation wahr. Zum Beispiel: "Ein Pferd frisst kein Heu" / A = 0, "Ein Pferd frisst kein Heu" (A = 1). Dies kann in Tabelle 3 ausgedrückt werden.

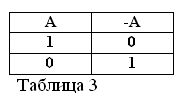
Um die Bedeutung der Negationsaktion zu bestimmen und anzunehmen, dass die beiden Aussagen A und / A immer eine Wahrheit sind, folgen zwei neue Formeln der Booleschen Algebra:

A + (/ A) = 1 und A * (/ A) = 0.

Es gibt auch andere Formeln, die die logische Verarbeitung von Anweisungen vereinfachen. Zum Beispiel ist 1 + A = 1, da gemäß der Definition der Addition in dem Fall, in dem ein Term gleich Eins ist, die Summe immer gleich Eins ist. Das erhaltene Ergebnis hängt nicht davon ab, ob A = 0 oder A = 1 ist.

Jede der drei von uns untersuchten logischen Operationen (AND, OR, NOT) hat bestimmte Eigenschaften, die den Regeln der Elementaralgebra nahe kommen. Wenn alle formuliert sind, erhalten wir 25 Regeln der Booleschen Algebra. Sie reichen völlig aus, um fast jedes logische Problem zu lösen. Ohne diese Regeln wird es aufgrund ihrer offensichtlichen Komplexität ziemlich schwierig, logische Probleme zu lösen. Der Versuch, die richtige Antwort zu finden, ohne die Regeln zu verwenden, bedeutet, sie durch Einfallsreichtum und allgemeine Argumentation zu ersetzen. Regeln erleichtern diese Arbeit erheblich und sparen Zeit.

Im Rahmen des Artikels ist es unmöglich, alle diese 25 Regeln zu berücksichtigen, aber diejenigen, die dies wünschen, können sie immer in der einschlägigen Literatur finden.

Wie bereits im ersten Artikel von 1938 erwähnt, verwendet der junge amerikanische Wissenschaftler Claude Shannon in seinem Artikel „Symbolische Analyse von Relais und Schaltkreisen“ erstmals die Boolesche Algebra für Probleme der Relaistechnologie. Shannons Entdeckung war, dass er erkannte, dass die Methode zum Entwerfen von Relaismaschinen und elektronischen Computern tatsächlich ein Zweig der mathematischen Logik ist.

Es kommt oft vor. Seit vielen Jahren arbeitet der Wissenschaftler an einem Problem, das seinen Landsleuten völlig unnötig erscheint - einfach nur Spaß. Aber Jahrzehnte und manchmal Jahrhunderte vergehen, und eine Theorie, die niemand braucht, erwirbt nicht nur das Existenzrecht, sondern ohne sie wird ein weiterer Fortschritt undenkbar.

Was hat Shannon beim zweiten Mal geholfen, die Boolesche Algebra zu „entdecken“? Fall? Nichts dergleichen.

Die Liebe zu Relaismaschinen, die auf herkömmlichen Schaltern und Relais basieren, half dem jungen Wissenschaftler, eine vergessene Theorie mit den Aufgaben der automatischen Telefonvermittlung zu verbinden, an denen er zu dieser Zeit arbeitete. Anschließend führte Shannon die gleiche Idee von „Ja oder Nein“ in diskrete Botschaften ein und legte den Grundstein für einen ganzen Abschnitt der Kybernetik - Informationstheorie.

Buhls Algebra war sehr gut für die Analyse und Synthese von Relaisschaltungen geeignet. Es genügte, als wahre Aussage zu akzeptieren: "Es gibt ein Signal in der Schaltung" und als falsches - "Es gibt kein Signal in der Schaltung", als eine neue Algebra erschien - die Signalalgebra, die Relaisschaltungsalgebra.

Die neue Algebra gilt nur für die Berücksichtigung von Relais- und Schaltkreisen. Schließlich ist nur in solchen Schemata die Bedingung "es gibt ein Signal" und "kein Signal" erfüllt. Wenn sich das Signal kontinuierlich ändert und eine beliebig große Anzahl von Zwischenbedingungen erfasst (ein solches Signal wird als analog bezeichnet), ist die Relaisalgebra nicht anwendbar. Dies muss immer beachtet werden. Aber nur die Mehrheit der elektronischen Computer und kybernetischen Maschinen verwendet das diskrete Prinzip der Signalverarbeitung, das auf den Elementen „Ja - Nein“ basiert.

Der Ausdruck "Kontakt geschlossen" wurde von Shannon als wahr (1) und "Kontakt offen" als falsch (0) akzeptiert. Den Rest der "Algebra", einschließlich der Operationen AND, OR und NOT und 25 Regeln, hat Shannon von Boole ausgeliehen.

Die Relaisschaltungsalgebra erwies sich als einfacher als die Boolesche Algebra, da sie nur Elemente vom Typ "Ja - Nein" behandelt. Darüber hinaus ist die neue Algebra visueller.

Die Elemente in dieser Algebra sind die Kontakte, die wir mit den Buchstaben A, B, C bezeichnen werden ... Der Kontakt ist geschlossen - A, der Kontakt ist offen - / A (Buchstabe mit einem Strich).

Wie Sie sehen, stammt die Notation vollständig aus der Booleschen Algebra. Ein offener Kontakt ist eine Negation eines geschlossenen Kontakts. Der gleiche Kontakt kann nicht sowohl geschlossen als auch offen sein.

Lassen Sie uns zustimmen, dass wenn in einem Stromkreis zwei Kontakte mit demselben Buchstaben bezeichnet werden, dies bedeutet, dass sie immer dieselben Werte annehmen.

Zu jedem Zeitpunkt sind entweder beide gleichzeitig geöffnet oder beide sind geschlossen. Der einfachste Weg, sich vorzustellen, dass sie mechanisch miteinander verbunden sind, so dass sich beide gleichzeitig öffnen oder schließen.

Wenn in einer Kette ein Kontakt eine Negation eines anderen Kontakts ist, sind ihre Bedeutungen immer entgegengesetzt. Beispielsweise können die Kontakte C und / C niemals gleichzeitig geöffnet oder gleichzeitig geschlossen werden. Und im Diagramm können sie mechanisch verbunden dargestellt werden: Wenn einer von ihnen öffnet, schließt der andere.

Wir beginnen unsere Bekanntschaft mit der Relaisalgebra, indem wir die einfachsten Schaltkreise analysieren, die den Operationen AND, OR und NOT entsprechen.

Das Produkt zweier Kontakte (Betrieb UND) ist der Stromkreis, der durch ihre Reihenschaltung erhalten wird: Er ist nur dann geschlossen (gleich 1), wenn beide Kontakte geschlossen sind (gleich 1).

Die Summe von zwei Kontakten (ODER-Betrieb) ist die Schaltung, die gebildet wird, wenn sie parallel geschaltet sind: Sie ist geschlossen (gleich 1), wenn mindestens einer der Kontakte, die die Schaltung bilden, geschlossen ist (gleich 1).

Das Gegenteil dieses Kontakts (Vorgang NICHT) ist ein Kontakt gleich 0 (offen), wenn dieser Kontakt 1 (geschlossen) ist, und umgekehrt.

Wie in der Booleschen Algebra bezeichnen wir, wenn die Kontakte mit den Buchstaben A und B bezeichnet sind, das Produkt zweier Kontakte mit A * B, die Summe mit A + B und den Kontakt gegenüber A mit / A. Das Obige wird in den 1, 2 und 3 erläutert.

Gültigkeit von Tabellen, die UND-, ODER- und NICHT-Operationen entsprechen. jetzt sollte niemand mehr zweifeln.

Lassen Sie uns auf zwei Beispiele eingehen: 1 * 0 = 0 und 1 + 0 = 1.

Aus der Abbildung ist ersichtlich, dass ein permanent geschlossener Kontakt, der in Reihe mit einem ständig offenen Kontakt geschaltet ist, einem permanent offenen Kontakt entspricht (1 * 0 = 0). Ein permanent geschlossener Kontakt, der parallel zu einem ständig offenen Kontakt geschaltet ist, entspricht einem permanent geschlossenen Kontakt.

Nachdem Sie sich mit der Arithmetik von Kontaktschaltungen vertraut gemacht haben, können Sie jede Relaisschaltung mit einer Formel unter Verwendung der akzeptierten Konventionen beschreiben. In der Kybernetik werden solche Formeln als strukturell bezeichnet.

Wenn die Strukturformel eines Relaisstromkreises 1 ist, kann ein Signal durch ihn hindurchgehen - der Stromkreis ist geschlossen. Wenn umgekehrt die Strukturformel der Schaltung 0 ist, wird das Signal nicht durchgelassen - die Schaltung ist unterbrochen.Schlussfolgerung: Zwei Relaisschaltungen sind einander äquivalent, wenn ihre Strukturformeln gleich sind.

In der Fortsetzung des Artikels werden Beispiele für Kontaktschaltungen, typische Kontaktschaltungen und deren Äquivalente betrachtet sowie Diagramme nach Strukturformeln erstellt. Wir betrachten auch die Hauptlogikschaltungen, die die Funktionen der Booleschen Algebra ausführen.

Fortsetzung des Artikels: Boolesche Algebra. Teil 3. Kontaktschemata

Boris Aladyshkin